Contents

Logistic regression

3.2. Logistic regression

Although having “regression” in its name, logistic regression is a classification (rather than regression) algorithm. Instead of modelling the qualitative response \(y\) directly, logistic regression models the probability that \(y\) belongs to a particular class (category).

Watch the 8-minute video below for a visual explanation of logistic regression:

Video

Explaining Logistic Regression by StatQuest, embedded according to YouTube’s Terms of Service.

3.2.1. Import libraries and load data

Get ready by importing the APIs needed from respective libraries.

import pandas as pd
import numpy as np
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, roc_auc_score, RocCurveDisplay

from statsmodels.formula.api import logit

%matplotlib inline

Load the Default dataset and inspect the first three rows.

data_url = "https://github.com/pykale/transparentML/raw/main/data/Default.csv"
df = pd.read_csv(data_url)

# Note: factorize() returns two objects: a label array and an array with the unique values. We are only interested in the first object.
df["default2"] = df.default.factorize()[0]
df["student2"] = df.student.factorize()[0]
df.head(3)
default student balance income default2 student2
0 No No 729.526495 44361.625074 0 0
1 No Yes 817.180407 12106.134700 0 1
2 No No 1073.549164 31767.138947 0 0

3.2.2. Logistic model

Logistic regression models the probability that the response \(y\) belongs to a particular class (category) using linear regression via a logistic function, hence the name logistic regression. For binary classification, let us use 1 to denote the positive class (e.g. “Yes”) and 0 to denote the negative class (e.g. “No”).

3.2.2.1. Logit function transformation

Let \(\pi\) be the probability of a positive outcome

\[ \pi = \mathbb{P}(y=1| x). \]

Then the probability of a negative outcome \( \mathbb{P}(y=0| x) = 1-\pi \).

The odds of a positive outcome is the ratio of the probability of a positive outcome to the probability of a negative outcome, i.e.

\[ \frac{\pi}{1-\pi}. \]

The log of the odds is called the logit and the logit function is defined as :

\[ \mathrm{logit}(\pi)=\log \frac{\pi}{1-\pi} \]

The logit function is a monotonic transformation of the probability \(\pi\). It maps the probability \(\pi\) ranging from 0 to 1 to the real line ranging from \(-\infty\) to \(\infty\). The logit function is also known as the log-odds function.

3.2.2.2. Logistic function

In simple linear regression, we have modelled the relationship between outcome \(y\) and feature \(x\) with a linear equation:

\[ y = \beta_0 + \beta_1 x. \]

This linear regression model is not able to produce a binary outcome for binary classification or a probability (in the range from 0 to 1 only). With the logit function above, we can transform the probability \(\pi\) ranging from 0 to 1 to the logit function \(\mathrm{logit}(\pi)\) ranging from \(-\infty\) to \(\infty\). Now we can use the linear regression model to model the logit function \(\mathrm{logit}(\pi)\) instead of the probability \(\pi\) or \(y\) directly. The logit function is defined as:

\[ \mathrm{logit}(\pi)=\log \frac{\pi}{1-\pi} = \beta_0 + \beta_1 x. \]

The logistic function, also known as the sigmoid function, is the inverse of the logit function. It maps the logit function \(\mathrm{logit}(\pi)\) ranging from \(-\infty\) to \(\infty\) to the probability \(\pi\) ranging from 0 to 1:

\[ \pi = \mathbb{P}(y = 1 | x) = \mathrm{logit}^{-1}(\beta_0 + \beta_1 x) = \mathrm{logistic}(\beta_0 + \beta_1 x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1)}}. \]

3.2.3. Estimating the coefficients to make predictions

The coefficients of a logistic regression model can be estimated by maximum likelihood estimation (MLE). The likelihood function is

\[ \mathcal{L}(\beta_0, \beta_1) = \prod_{i:y_i=1} \mathbb{P}(y_i = 1) \prod_{i:y_i=0} (1 - \mathbb{P}(y_i = 1)). \]

The mathematical details are beyond the scope of this course. If interested, please read Section 4.3 of the Pattern Recognition and Machine Learning book for more details of the optimization for logistic regression.

To make predictions, taking the classification problem on the Default dataset, the probability of default given balance predicted by a logistic regression model is

\[ \mathbb{P}(\text{default} = \text{Yes} \mid \text{balance}, \beta_0, \beta_1) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 \times \text{balance})}}. \]

3.2.3.1. Example explanation of system transparency

Let us to see the curve of the logistic function on the Default dataset.

sns.regplot(data=df, x="balance", y="default2", logistic=True)
plt.ylabel("Probability of default")
plt.xlabel("Balance")
plt.show()
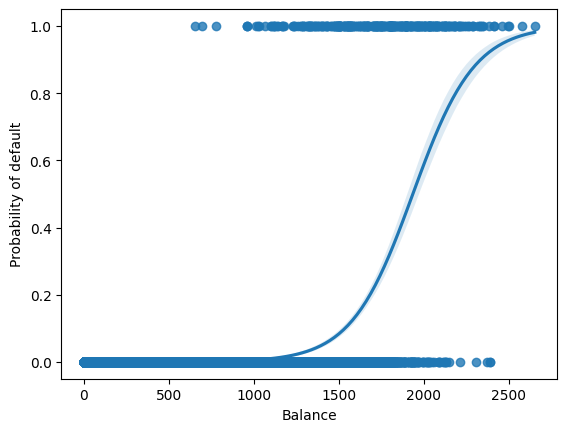
../_images/logistic-regression_7_0.png

We can see an S-shaped curve with the vertical axis ranging from 0 to 1, indicating the probability of a positive outcome (default) with respect to the horizontal axis \(x\) (balance).

In practice, we can use the scikit-learn or statsmodels package to fit a logistic regression model and make predictions.

Let us fit a logistic regression model using the scikit-learn API for logistic regression first.

clf = LogisticRegression(solver="newton-cg")
X_train = df.balance.values.reshape(-1, 1)
X_test = np.arange(df.balance.min(), df.balance.max()).reshape(-1, 1)
y = df.default2
clf.fit(X_train, y)
print(clf)
print("classes: ", clf.classes_)
print("coefficients: ", clf.coef_)
print("intercept :", clf.intercept_)

LogisticRegression(solver='newton-cg')
classes:  [0 1]
coefficients:  [[0.00549892]]
intercept : [-10.65132978]

Let us plot the fitted logistic regression model and study the system transparency.

prob = clf.predict_proba(X_test)

plt.scatter(X_train, y, color="orange")
plt.plot(X_test, prob[:, 1], color="lightblue")

plt.hlines(
    1,
    xmin=plt.gca().xaxis.get_data_interval()[0],
    xmax=plt.gca().xaxis.get_data_interval()[1],
    linestyles="dashed",
    lw=1,
)
plt.hlines(
    0,
    xmin=plt.gca().xaxis.get_data_interval()[0],
    xmax=plt.gca().xaxis.get_data_interval()[1],
    linestyles="dashed",
    lw=1,
)

plt.hlines(
    0.5,
    xmin=plt.gca().xaxis.get_data_interval()[0],
    xmax=plt.gca().xaxis.get_data_interval()[1],
    linestyles="dashed",
    lw=1,
)

plt.vlines(
    -clf.intercept_ / clf.coef_[0],
    ymin=plt.gca().yaxis.get_data_interval()[0],
    ymax=plt.gca().yaxis.get_data_interval()[1],
    linestyles="dashed",
    lw=1,
)

plt.hlines(
    (clf.predict_proba(np.asarray(1500).reshape(-1, 1)))[0][1],
    xmin=plt.gca().xaxis.get_data_interval()[0],
    xmax=1500,
    linestyles="dashed",
    lw=1,
)

plt.vlines(
    1500,
    ymin=plt.gca().yaxis.get_data_interval()[0],
    ymax=(clf.predict_proba(np.asarray(1500).reshape(-1, 1)))[0][1],
    linestyles="dashed",
    lw=1,
)

plt.ylabel("Probability of default")
plt.xlabel("Balance")
plt.yticks([0, 0.25, 0.5, 0.75, 1.0])
plt.xlim(xmin=-100)
plt.show()
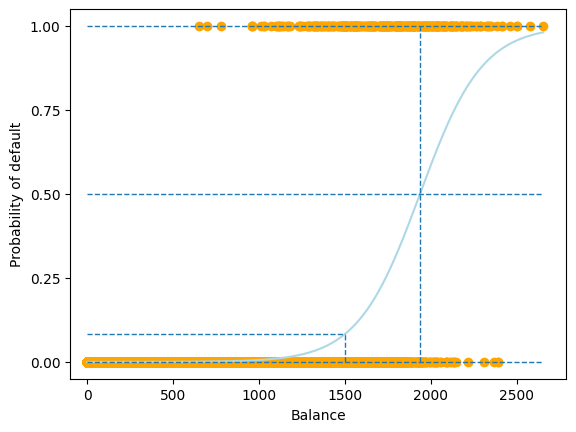
../_images/logistic-regression_11_0.png

In the above example, we learnt a logistic regression model \(f(x)\) with two parameters, \(\beta_0\) and \(\beta_1\), from the data, where

  • \(\beta_0 = -10.65133019 \)

  • \(\beta_1 = 0.00549892 \)

Using these two estimated parameters, we can examine the system logic of the logistic regression model to reveal its system transparency.

System transparency

  • When balance=1500 , the predicted probability of default is

\[ f(1500) = \frac{1}{1 + e^{\beta_0 + \beta_1 \times 1500}} = \frac{1}{1 + e^{-10.65133019 + 0.00549892 \times 1500}} = 0.08294763. \]

  • When the probability of default 0.5 (the commonly used threshold for binary classification), the corresponding balance can be calculated using the log odds equation above:

(3.1)\[\begin{align} \begin{aligned} \ln \left(\frac{\pi}{1-\pi}\right) &= \beta_0 + \beta_1 \times x \\ \ln \left(\frac{0.5}{1-0.5}\right) &= \beta_0 + \beta_1 \times x \\ x & = \frac{- \beta_0}{\beta_1} \\ x & = \frac{- (-10.65133019)}{0.00549892} \\ x & = 1936.9858426745614. \end{aligned} \end{align}\]

Therefore, to produce result Yes, i.e. for the probability of default \(>\) 0.5, the balance should be greater than 1936.9858426745614. Likewise, to produce result No, i.e. the probability of default \(<\) 0.5, the balance should be less than 1936.9858426745614.

Let us fit a logistic regression model using the [statsmodels API for logistic regression] next.

est = logit("default2 ~ balance", df).fit()
est.summary2().tables[1]

Optimization terminated successfully.
         Current function value: 0.079823
         Iterations 10
Coef. Std.Err. z P>|z| [0.025 0.975]
Intercept -10.651331 0.361169 -29.491287 3.723665e-191 -11.359208 -9.943453
balance 0.005499 0.000220 24.952404 2.010855e-137 0.005067 0.005931

We can see that the estimated parameters are the same as those from the scikit-learn API. Note the two last columns, “[0.025” and “0.975]”. These are Confidence Intervals, the very concept we covered in the last chapter on Linear Regression! Now, let us fit a logistic regression model using student status as the input variable.

est = logit("default2 ~ student", df).fit()
est.summary2().tables[1]

Optimization terminated successfully.
         Current function value: 0.145434
         Iterations 7
Coef. Std.Err. z P>|z| [0.025 0.975]
Intercept -3.504128 0.070713 -49.554094 0.000000 -3.642723 -3.365532
student[T.Yes] 0.404887 0.115019 3.520177 0.000431 0.179454 0.630320

The coefficient associated with student is positive, indicating that the probability of default is higher for students than non-students.

3.2.4. Multiple logistic regression

The logistic regression model can be extended to multiple features. A generalised logistic regression model for an instance \(\mathbf{x} = [x_1, x_2, \dots, x_D]^\top\) is

\[ \ln \left( \frac{\pi}{1-\pi} \right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_D x_D. \]

Let us fit a multiple logistic regression model using the scikit-learn API first.

Let us plot the fitted multiple logistic regression model and study the system transparency.

import warnings

warnings.filterwarnings("ignore")

X_train = df.loc[:, ["balance", "income", "student2"]]
y = df.default2

clf = LogisticRegression(solver="newton-cg", penalty="none", max_iter=1000)
clf.fit(X_train, y)
print(clf)
print("classes: ", clf.classes_)
print("coefficients: ", clf.coef_)
print("intercept :", clf.intercept_)

LogisticRegression(max_iter=1000, penalty='none', solver='newton-cg')
classes:  [0 1]
coefficients:  [[ 5.73139387e-03  2.83615167e-06 -6.51143222e-01]]
intercept : [-10.85258456]

Let us fit a multiple logistic regression model using the statsmodels API next.

est = logit("default2 ~ balance + income + student", df).fit()
est.summary2().tables[1]

Optimization terminated successfully.
         Current function value: 0.078577
         Iterations 10
Coef. Std.Err. z P>|z| [0.025 0.975]
Intercept -10.869045 0.492273 -22.079320 4.995499e-108 -11.833882 -9.904209
student[T.Yes] -0.646776 0.236257 -2.737595 6.189022e-03 -1.109831 -0.183721
balance 0.005737 0.000232 24.736506 4.331521e-135 0.005282 0.006191
income 0.000003 0.000008 0.369808 7.115254e-01 -0.000013 0.000019

Similar parameters are estimated as using the scikit-learn API.

3.2.5. Evaluation of logistic regression

The evaluation of logistic regression is similar to the evaluation of linear regression. The main difference is that the evaluation metrics are different. For example, the mean squared error (MSE) is not a good metric for classification. Here we introduce two common metrics for classification: accuracy and area under receiver operating characteristic (ROC) curve, i.e. AUC (or more precisely, AUROC).

3.2.5.1. Accuracy

The accuracy is the fraction of correct predictions. It is defined as

\[ \text{accuracy} = \frac{\text{number of correct predictions}}{\text{total number of predictions}}. \]

Let us compute the training accuracy of the multiple logistic regression model trained using scikit-learn API above.

y_pred = clf.predict(X_train)
accuarcy = accuracy_score(y, y_pred)
print("Accuracy: ", accuarcy)

Accuracy:  0.9732

3.2.5.2. Area under the ROC curve (AUC)

The receiver operating characteristic (ROC) curve is a plot of the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. The TPR and FPR are defined as

\[\begin{split} \begin{aligned} \text{TPR} &= \frac{\text{number of true positives}}{\text{number of positives}} \\ \text{FPR} &= \frac{\text{number of false positives}}{\text{number of negatives}} \end{aligned} \end{split}\]

The area under the ROC curve (AUC) is a popular measure of classifier performance. The AUC is defined as the area under the ROC curve. It is a number between 0 and 1, where 0.5 is the random guess and 1 is the perfect prediction. The AUC is a good metric for evaluating the classification since it considers all possible classification thresholds.

Let us plot the ROC curve of the multiple logistic regression model trained using scikit-learn API above.

y_prob = clf.predict_proba(X_train)[:, 1]

roc_auc = roc_auc_score(y, y_prob)
print("AUC: ", roc_auc)

clf_disp = RocCurveDisplay.from_estimator(clf, X_train, y)
plt.show()

AUC:  0.949552531739353
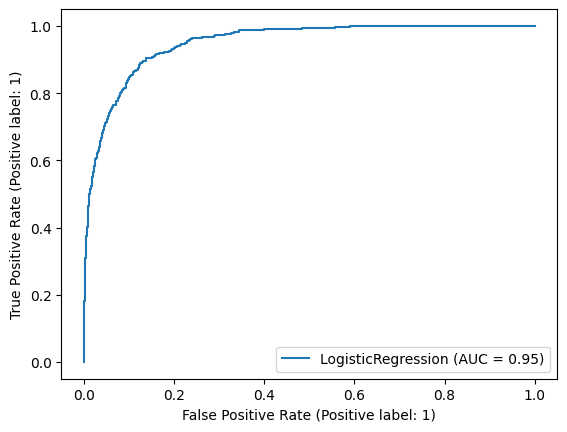
../_images/logistic-regression_26_1.png

We can see clearly the trade-off between TPR and FPR. The AUC is 0.95, indicating that the model is good.

3.2.6. Exercise

1. Logistic regression is a classification algorithm.

    a. True
    
    b. False

Compare your answer with the solution below

a. True

2. All the following exercises will use the Weekly dataset.

Load the dataset, convert the categories to numerical values, and fit a logistic regression model using Volume variable as a predictor and Direction variable as the response using scikit-learn or statsmodel. Find out the fitted model’s weight and bias.

# Write your code below to answer the question

Compare your answer with the reference solution below

import pandas as pd
import numpy as np
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.linear_model import LogisticRegression


data_url = "https://github.com/pykale/transparentML/raw/main/data/Weekly.csv"
df = pd.read_csv(data_url)
df["Direction"] = df.Direction.factorize()[0]

clf = LogisticRegression(solver="newton-cg")
X_train = df.Volume.values.reshape(-1, 1)
y = df.Direction
clf.fit(X_train, y)
print("coefficients: ", clf.coef_)
print("intercept :", clf.intercept_)

coefficients:  [[-0.0213956]]
intercept : [0.25689958]

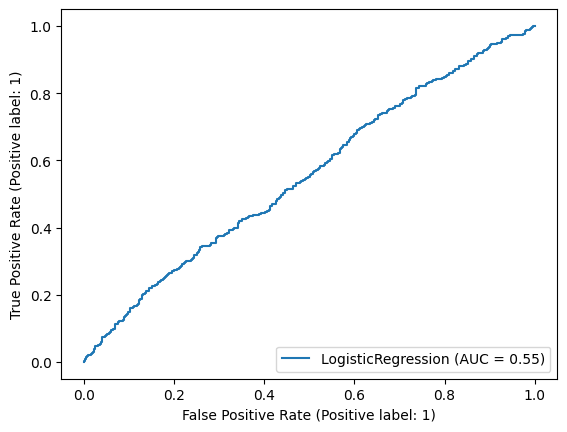
3. Plot the ROC curve and find out the training accuracy and AUC of the fitted model from Exercise 2.

# Write your code below to answer the question

Compare your answer with the reference solution below

from sklearn.metrics import accuracy_score, roc_auc_score, RocCurveDisplay

y_pred = clf.predict(X_train)
accuarcy = accuracy_score(y, y_pred)
print("Training Accuracy: ", accuarcy)

y_prob = clf.predict_proba(X_train)[:, 1]
roc_auc = roc_auc_score(y, y_prob)
print("AUC: ", roc_auc)

clf_disp = RocCurveDisplay.from_estimator(clf, X_train, y)
plt.show()

# From the ROC curve we can say that the result is almost random as it is almost close to 50%.
# The model from Exercise-2 has not learnt anything at all.

Training Accuracy:  0.5555555555555556
AUC:  0.5142783962844069
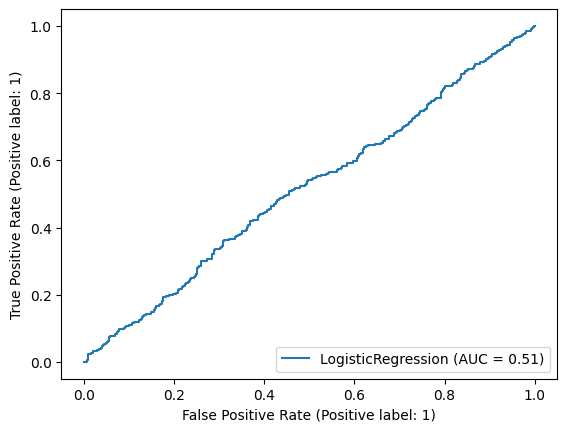
../_images/logistic-regression_39_1.png

4. Train another logistic regression model using Direction as a response and all the other features as predictors. Print out all the parameter values.

# Write your code below to answer the question

Compare your answer with the reference solution below

X_train = df.drop(["Direction"], axis=1)

y = df.Direction

clf = LogisticRegression(solver="newton-cg")
clf.fit(X_train, y)
print("coefficients: ", clf.coef_)
print("intercept :", clf.intercept_)

coefficients:  [[ 3.68485224e-03 -8.79795063e-02  4.30643833e-02  1.39945670e-02
  -1.71842138e-02  6.21526979e-02  7.95815168e-02  7.22161831e+00]]
intercept : [-7.36769879]

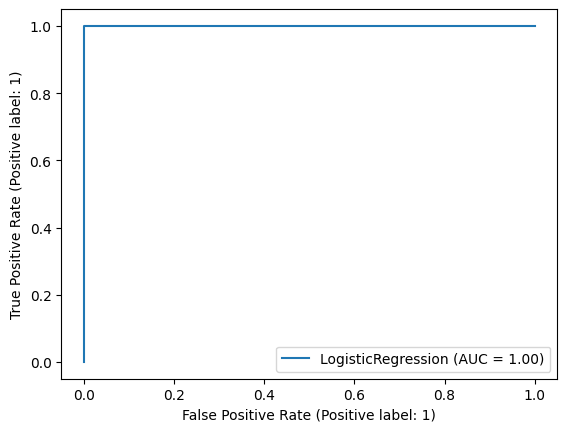
5. Plot the ROC curve and find out the training accuracy and AUC metrics of the fitted model from Exercise 4.

# Write your code below to answer the question

Compare your answer with the reference solution below

y_pred = clf.predict(X_train)
accuarcy = accuracy_score(y, y_pred)
print("Training Accuracy: ", accuarcy)

y_prob = clf.predict_proba(X_train)[:, 1]
roc_auc = roc_auc_score(y, y_prob)
print("AUC: ", roc_auc)

clf_disp = RocCurveDisplay.from_estimator(clf, X_train, y)
plt.show()

# The model from Exercise 4 learnt very well on the training dataset.

Training Accuracy:  0.9972451790633609

AUC:  0.9999931698654464
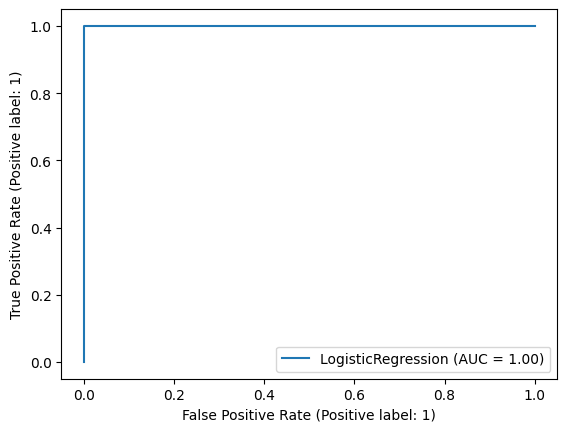
../_images/logistic-regression_47_2.png

6. You might notice that the model with all variables is much better than the model from Exercise 2. Use the skills you have learnt to perform further analysis on the data to explain why. Hint: Consider correlations (See section 2.2.4)

# Write your code below to answer the question

Compare your answer with the reference solution below

corr_matrix = df.corr()
print(corr_matrix)
# Here from the correlation result we can see that, "Today" has a 0.72 correlation with "Direction"
# which is the main reason for getting high performance

y = df.Direction

# model with out "Today"
X_train = df.drop(["Direction", "Today"], axis=1)
clf.fit(X_train, y)
clf_disp = RocCurveDisplay.from_estimator(clf, X_train, y)
# Without today feature the model performed very bad

# model with only "Today"
X_train = df["Today"].values.reshape(-1, 1)
clf.fit(X_train, y)
clf_disp = RocCurveDisplay.from_estimator(clf, X_train, y)
# with today feature the model performed very well
# from this experiment we analyzed the important of correlation between feature and target variable

               Year      Lag1      Lag2      Lag3      Lag4      Lag5  \
Year       1.000000 -0.032289 -0.033390 -0.030006 -0.031128 -0.030519   
Lag1      -0.032289  1.000000 -0.074853  0.058636 -0.071274 -0.008183   
Lag2      -0.033390 -0.074853  1.000000 -0.075721  0.058382 -0.072499   
Lag3      -0.030006  0.058636 -0.075721  1.000000 -0.075396  0.060657   
Lag4      -0.031128 -0.071274  0.058382 -0.075396  1.000000 -0.075675   
Lag5      -0.030519 -0.008183 -0.072499  0.060657 -0.075675  1.000000   
Volume     0.841942 -0.064951 -0.085513 -0.069288 -0.061075 -0.058517   
Today     -0.032460 -0.075032  0.059167 -0.071244 -0.007826  0.011013   
Direction -0.022200 -0.050004  0.072696 -0.022913 -0.020549 -0.018168   

             Volume     Today  Direction  
Year       0.841942 -0.032460  -0.022200  
Lag1      -0.064951 -0.075032  -0.050004  
Lag2      -0.085513  0.059167   0.072696  
Lag3      -0.069288 -0.071244  -0.022913  
Lag4      -0.061075 -0.007826  -0.020549  
Lag5      -0.058517  0.011013  -0.018168  
Volume     1.000000 -0.033078  -0.017995  
Today     -0.033078  1.000000   0.720025  
Direction -0.017995  0.720025   1.000000
../_images/logistic-regression_51_1.png ../_images/logistic-regression_51_2.png

previous

3.1. Regression model for classification?

next

3.3. Quiz and summary