# probabilistic programming
import pyro 

# MCMC plotting
import arviz as az
import matplotlib.pyplot as plt
from getdist import plots

# autoemulate imports
from autoemulate.calibration.interval_excursion_set import IntervalExcursionSetCalibration
from autoemulate.core.compare import AutoEmulate
from autoemulate.data.utils import set_random_seed
from autoemulate.simulations.projectile import Projectile
from autoemulate.emulators.gaussian_process.exact import GaussianProcessRBF

# suppress warnings in notebook for readability
import os
import warnings

# ignore warnings
warnings.filterwarnings("ignore")
os.environ["PYTHONWARNINGS"] = "ignore"

# random seed for reproducibility
random_seed = 42
set_random_seed(random_seed)
pyro.set_rng_seed(random_seed)

Interval Excursion Set

In this tutorial we will demonstrate how to use AutoEmulate to estimate the interval excursion set of a simulator. The interval excursion set is the set of input parameters for which the simulator output lies within a specified interval. This is a more general problem than estimating level sets, superlevel sets, or sublevel sets, as it allows for the specification of both lower and upper bounds on the output.

We will use the Projectile simulator from the previous tutorials. We will first generate training data and fit a Gaussian process (GP) model to the data. We will then formulate the interval excursion set as a probabilistic model and then use the IntervalExcursionSetCalibration class to estimate the interval excursion set using both gradient-based MCMC (NUTS) and Sequential Monte Carlo (SMC) sampling methods.

Projectile simulation: run simulator and fit emulator

To begin with we create a simulator and generate some training data, before fitting a Gaussian process (GP) emulator to the data using AutoEmulate.

# Create simulator and generate training data
simulator = Projectile(
    parameters_range={"c": (-5.0, 1.0), "v0": (0.0, 10.0)},
    log_level="error"
)
x = simulator.sample_inputs(1000)
y, _ = simulator.forward_batch(x)

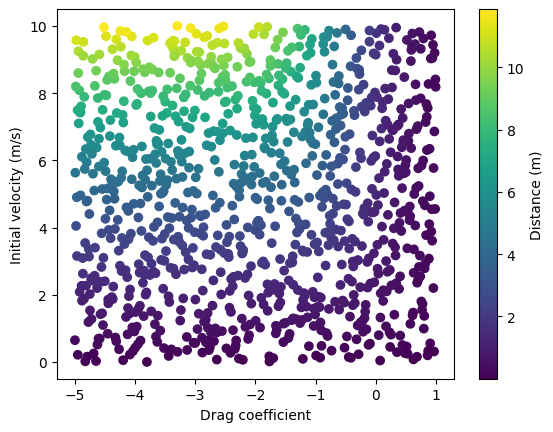
# Visualize training data
c = x[:, 0]
v0 = x[:, 1]
plt.scatter(c, v0, c=y[:, 0], cmap='viridis')
plt.xlabel('Drag coefficient')
plt.ylabel('Initial velocity (m/s)')
plt.colorbar(label="Distance (m)")
plt.show()

# Run AutoEmulate to find the best GP model
ae = AutoEmulate(
    x, 
    y, 
    models=[GaussianProcessRBF],
    model_params={},
    log_level="error", 
)

# Get best GP model
gp = ae.best_result().model

Problem set-up: identify an interval excursion set for \(f(x)\)

The aim for the remainder of this notebook is to explore methods that are able to identify samples \(x\) from the interval excursion set.

Mathematically this is:

\[ x \in \mathbb{R}^n, \quad a, b \in \mathbb{R}^m, \quad f: \mathbb{R}^n \to \mathbb{R}^m, \quad a_i < f_i(x) < b_i \;\; \forall i \in I \subseteq \{1,\dots,m\} \]

with the interval excursion defined as:

\[ \text{Interval Excursion Set (IES):} \quad \mathrm{IES}_{a,b,I} := \{\, x \in \mathbb{R}^n : a_i < f_i(x) < b_i \;\; \forall i \in I \,\}. \ \]

The interval excursion set encompasses, as special cases, several familiar constructions:

• the level set defined by \(f(x) = c\),

• the superlevel set defined by \(f(x) > c\), and

• the sublevel set defined by \(f(x) < c\).

The probability that a Gaussian random variable \(y \sim \mathcal{N}(\mu, \sigma^2)\) lies in the interval \(a < y < b\) is:

\[ P(a < y < b) = \Phi\left(\frac{b - \mu}{\sigma}\right) - \Phi\left(\frac{a - \mu}{\sigma}\right) \]

where \(\Phi(\cdot)\) is the cumulative distribution function (CDF) of the standard normal distribution.

In the Bayesian setting, this interval probability is used as a likelihood function. The posterior density for \(x\) is then proportional to the product of the prior \(p(x)\) and the probability that the model output \(f(x)\) lies in the interval \(a < y < b\):

\[p(x \mid a < f(x) < b) \propto p(x) \left[ \Phi\left(\frac{b - \mu(x)}{\sigma(x)}\right) - \Phi\left(\frac{a - \mu(x)}{\sigma(x)}\right) \right]\]

where \(\mu(x)\) and \(\sigma(x)\) are the mean and standard deviation of the model output at \(x\).

lower, upper = 6.0, 8.0
ies = IntervalExcursionSetCalibration(
    gp,
    parameters_range=simulator.parameters_range,
    output_bounds={"distance": (lower, upper)},
    output_names=simulator.output_names,
    log_level="error",
)

Interval excursion set samples using MCMC

We next run the MCMC sampler. By default, it uses NUTS here, but Metropolis can also produce reasonable samples for low-dimensional parameter spaces, as is the case in this projectile simulator model.

mcmc = ies.run_mcmc(
    num_samples=500,
    warmup_steps=200,
    num_chains=2,
    sampler="nuts",
    # sampler="metropolis",
    model_kwargs={"uniform_prior": True}
)
az_mcmc = ies.to_arviz(mcmc)

Draw posterior predictive samples.

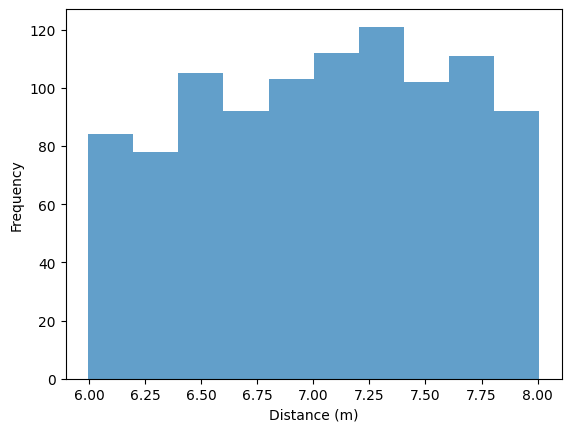
y_pred = ies.posterior_predictive(mcmc)
plt.hist(y_pred["distance"], density=False, alpha=0.7)
plt.xlabel("Distance (m)")
plt.ylabel("Frequency")
plt.show()

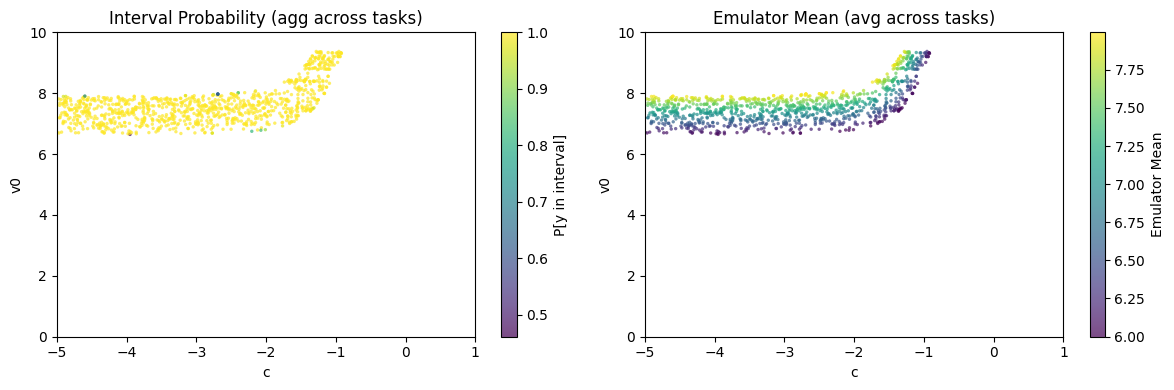
Plot likelihood and mean of MCMC samples.

ies.plot_samples(az_mcmc)

Convert to arviz InferenceData object for further analysis, such as plot_posterior().

az_data = ies.to_arviz(mcmc)
_ = az.plot_posterior(az_data)

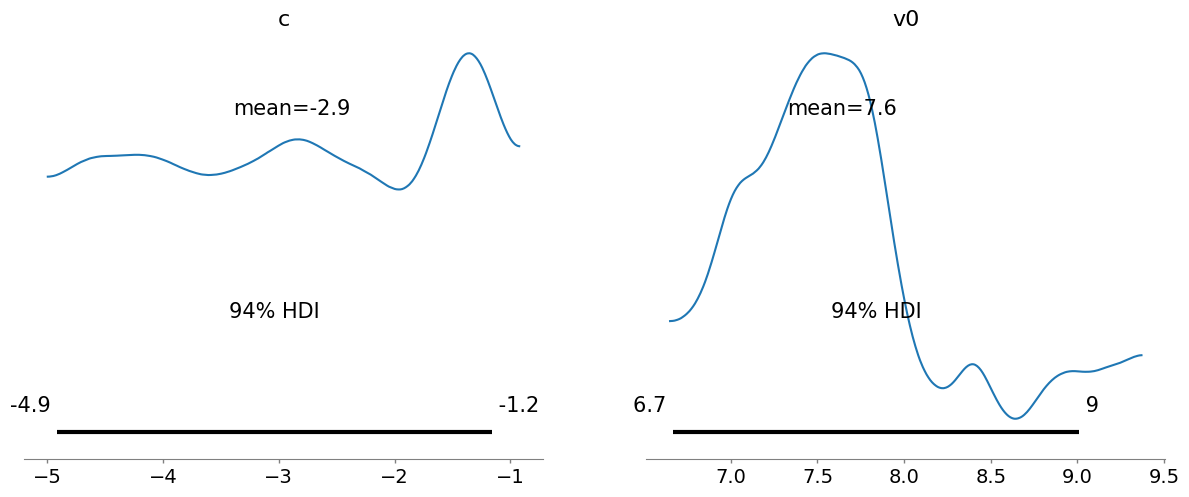
GetDist can also be used to create a plot of posterior sample densities.

def get_dist_and_plot(ies, data):
    """Convert and plot GetDist MCSamples from MCMC samples."""
    emu_data = ies.to_getdist(data, label="Emulator")
    emu_data.smooth_scale_1D = 0.8
    g = plots.get_subplot_plotter()
    g.triangle_plot([emu_data], filled=True)
    plt.show()

get_dist_and_plot(ies, mcmc)

Removed no burn in

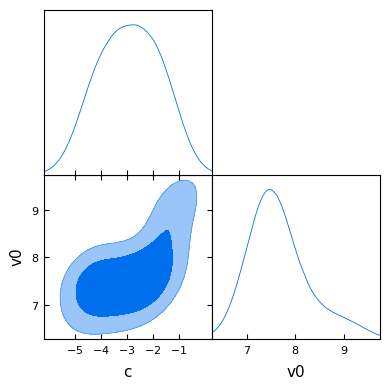
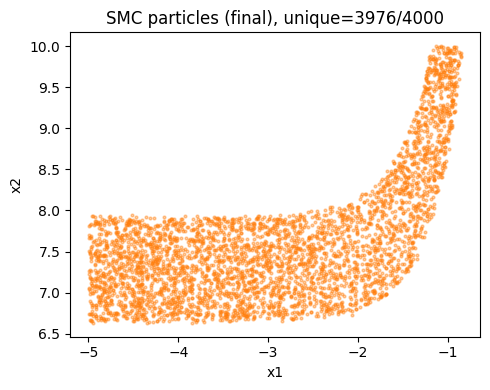
Interval excursion set samples using SMC with adaptive tempering

The Sequential Monte Carlo (SMC) implementation provides an alternative to MCMC approaches.

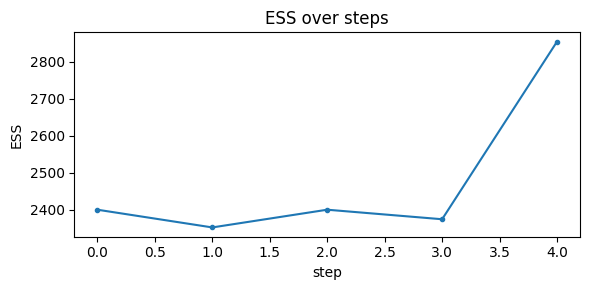
It works by tempering the interval excursion set likelihood from 0 to 1 (i.e. sampling from the prior to the posterior), adaptively controlling steps to hit a target Effective Sample Size (ESS). We resample when ESS falls below the threshold. This converges to the exact target at temperature 1 without gradients.

# Run SMC and plot diagnostics
az_data_smc = ies.run_smc(
    n_particles=4000,
    ess_target_frac=0.6,
    move_steps=2,
    rw_step=0.25,
    seed=random_seed,
    uniform_prior=True,
    plot_diagnostics=True,
    return_az_data=True
)

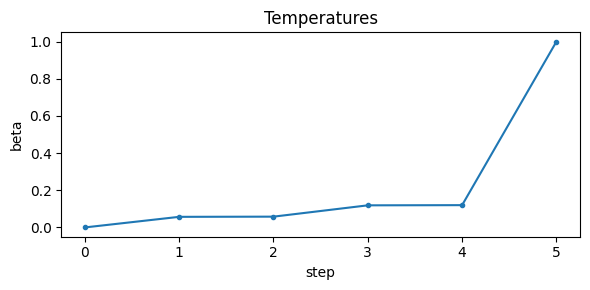
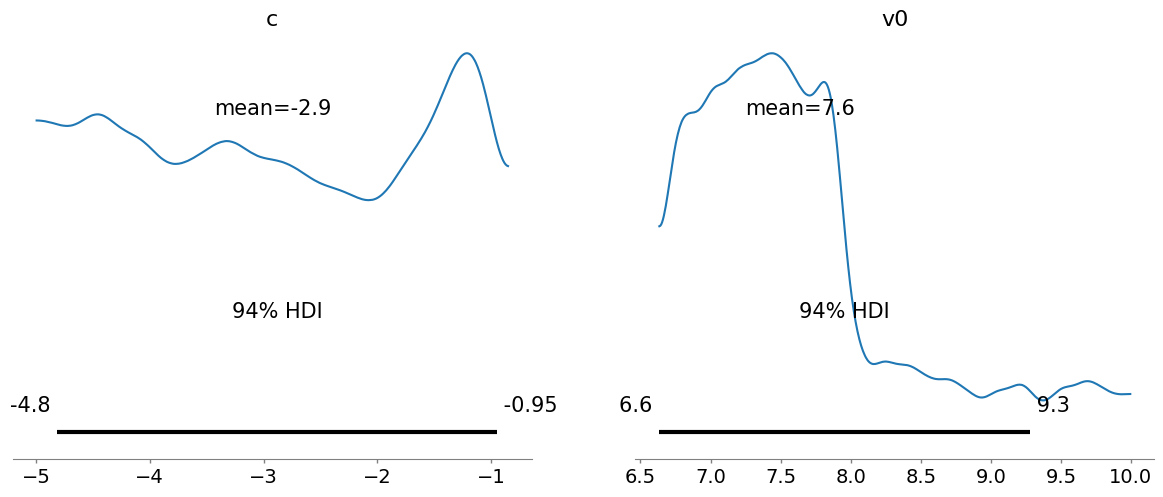
plot_posterior() for SMC samples.

_ = az.plot_posterior(az_data_smc)

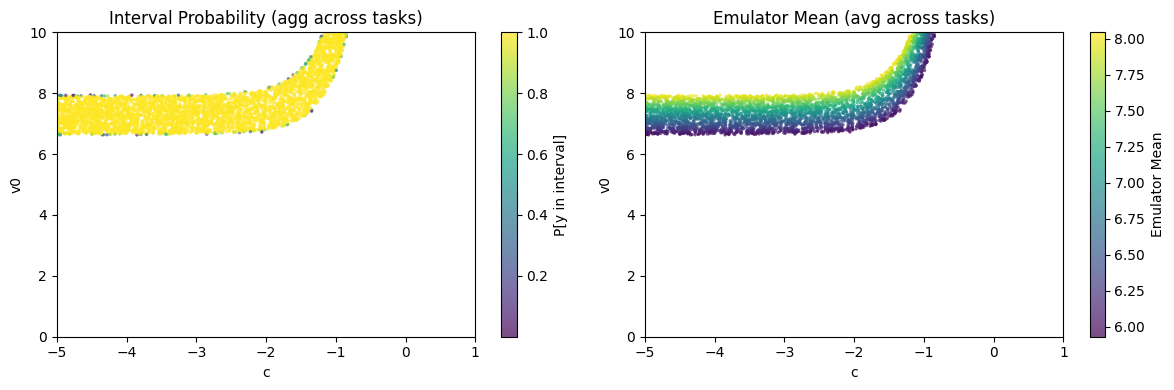
Plot the likelihood and values of SMC samples.

assert isinstance(az_data_smc, az.InferenceData)
ies.plot_samples(az_data_smc)

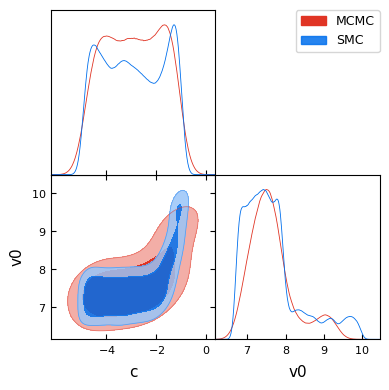
And finally a GetDist plot comparing the MCMC and SMC posterior sample densities. Some differences are expected due to the different sampling approaches, but overall the posterior sample densities are similar.

assert isinstance(az_data_smc, az.InferenceData)
g = plots.get_subplot_plotter()
_ = g.triangle_plot( 
    [ies.to_getdist(az_mcmc, "MCMC"), ies.to_getdist(az_data_smc, "SMC")],
    filled=True,
)

Removed no burn in
Removed no burn in