5.1 How to test#

Estimated time for this notebook: 15 minutes

Choosing the scenarios to test - “Equivalence partitioning”#

Think hard about the different cases the code will run under: this is science, not coding!

We can’t write a test for every possible input: this is an infinite amount of work.

We need to write tests to rule out different bugs. There’s no need to separately test equivalent inputs.

Let’s look at an example of this question outside of coding:

  • Research Project : Evolution of agricultural fields in Saskatchewan from aerial photography

  • In silico translation : Compute overlap of two rectangles

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import patches
from matplotlib.path import Path

Let’s make a little fragment of matplotlib code to visualise a pair of fields.

def show_fields(field1, field2):
    def vertices(left, bottom, right, top):
        verts = [
            (left, bottom),
            (left, top),
            (right, top),
            (right, bottom),
            (left, bottom),
        ]
        return verts

    codes = [Path.MOVETO, Path.LINETO, Path.LINETO, Path.LINETO, Path.CLOSEPOLY]
    path1 = Path(vertices(*field1), codes)
    path2 = Path(vertices(*field2), codes)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    patch1 = patches.PathPatch(path1, facecolor="orange", lw=2)
    patch2 = patches.PathPatch(path2, facecolor="blue", lw=2)
    ax.add_patch(patch1)
    ax.add_patch(patch2)
    ax.set_xlim(0, 5)
    ax.set_ylim(0, 5)


show_fields((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 3.0))
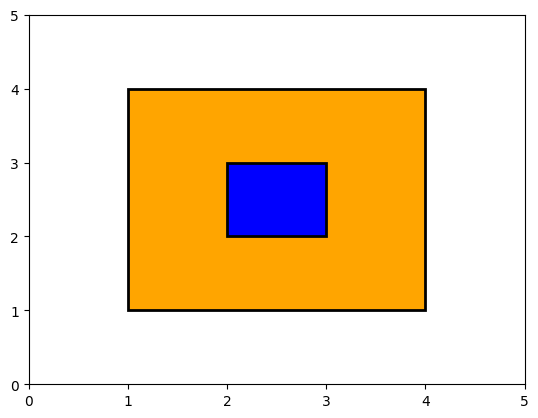
../_images/05_01_how_to_test_10_0.png

Here, we can see that the area of overlap, is the same as the smaller field, with area 1.

We could now go ahead and write a subroutine to calculate that, and also write some test cases for our answer.

But first, let’s just consider that question abstractly, what other cases, not equivalent to this might there be?

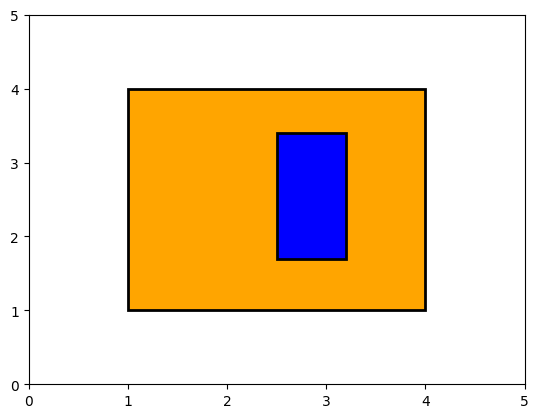
For example, this case, is still just a full overlap, and is sufficiently equivalent that it’s not worth another test:

show_fields((1.0, 1.0, 4.0, 4.0), (2.5, 1.7, 3.2, 3.4))
../_images/05_01_how_to_test_15_0.png

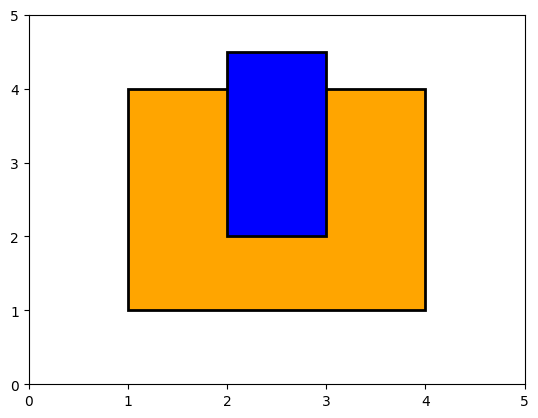
But this case is no longer a full overlap, and should be tested separately:

show_fields((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 4.5))
../_images/05_01_how_to_test_17_0.png

On a piece of paper, sketch now the other cases you think should be treated as non-equivalent. Some answers are below:

for _ in range(50):
    print("Spoiler space")

Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space
Spoiler space

show_fields((1.0, 1.0, 4.0, 4.0), (2, 2, 4.5, 4.5))  # Overlap corner
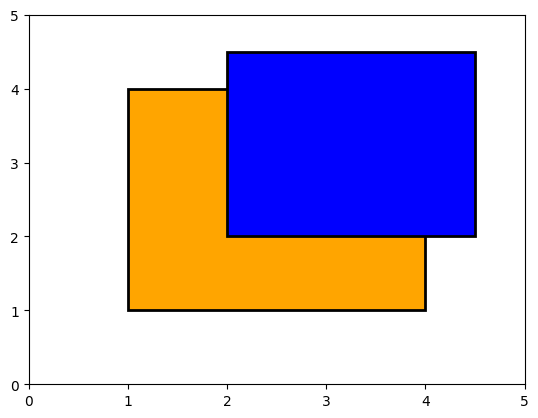
../_images/05_01_how_to_test_20_0.png 
show_fields((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 4.0))  # Just touching
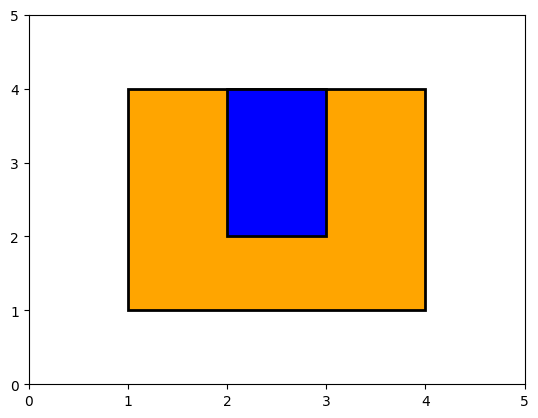
../_images/05_01_how_to_test_21_0.png 
show_fields((1.0, 1.0, 4.0, 4.0), (4.5, 4.5, 5, 5))  # No overlap
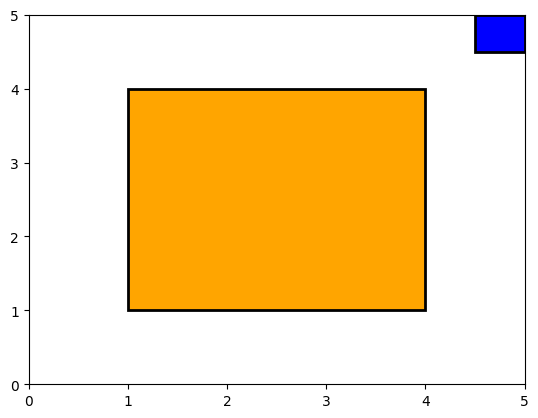
../_images/05_01_how_to_test_22_0.png 
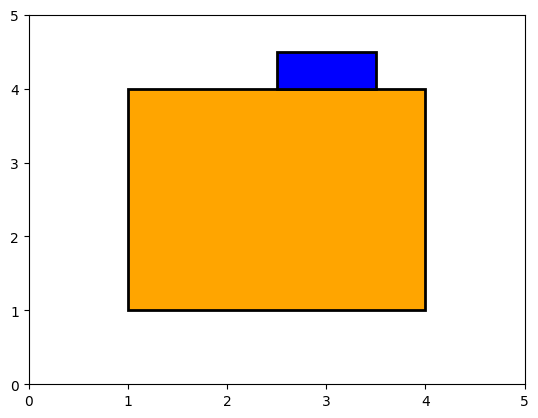
show_fields((1.0, 1.0, 4.0, 4.0), (2.5, 4, 3.5, 4.5))  # Just touching from outside
../_images/05_01_how_to_test_23_0.png 
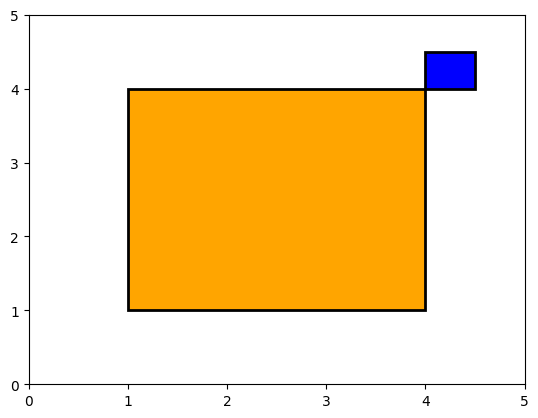
show_fields((1.0, 1.0, 4.0, 4.0), (4, 4, 4.5, 4.5))  # Touching corner
../_images/05_01_how_to_test_24_0.png

Using our tests#

OK, so how might our tests be useful?

Here’s some code that might correctly calculate the area of overlap:

def overlap(field1, field2):
    left1, bottom1, top1, right1 = field1
    left2, bottom2, top2, right2 = field2
    overlap_left = max(left1, left2)
    overlap_bottom = max(bottom1, bottom2)
    overlap_right = min(right1, right2)
    overlap_top = min(top1, top2)
    overlap_height = overlap_top - overlap_bottom
    overlap_width = overlap_right - overlap_left
    return overlap_height * overlap_width

So how do we check our code?

The manual approach would be to look at some cases, and, once, run it and check:

overlap((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 3.0))

1.0

That looks OK.

But we can do better - we don’t want to have to manually check our results. We can use the assert statement for this:

assert <some statement>

If <some statement> evaluate to True carry on. If not, raise an error.

assert overlap((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 3.0)) == 1.0

assert overlap((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 3.0, 4.5)) == 2.0

assert overlap((1.0, 1.0, 4.0, 4.0), (2.0, 2.0, 4.5, 4.5)) == 4.0

assert overlap((1.0, 1.0, 4.0, 4.0), (4.5, 4.5, 5, 5)) == 0.0

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[16], line 1
----> 1 assert overlap((1.0, 1.0, 4.0, 4.0), (4.5, 4.5, 5, 5)) == 0.0

AssertionError: 

print(overlap((1.0, 1.0, 4.0, 4.0), (4.5, 4.5, 5, 5)))

0.25

show_fields((1.0, 1.0, 4.0, 4.0), (4.5, 4.5, 5, 5))
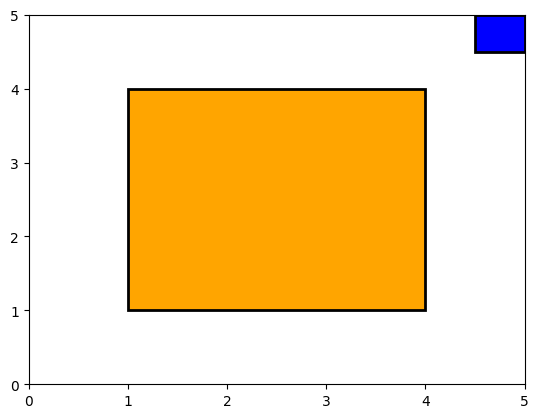
../_images/05_01_how_to_test_39_0.png

What? Why is this wrong?

In our calculation, we are actually getting:

overlap_left = 4.5
overlap_right = 4
overlap_width = -0.5
overlap_height = -0.5

Both width and height are negative, resulting in a positive area. The above code didn’t take into account the non-overlap correctly.

It should be:

def overlap(field1, field2):
    left1, bottom1, top1, right1 = field1
    left2, bottom2, top2, right2 = field2

    overlap_left = max(left1, left2)
    overlap_bottom = max(bottom1, bottom2)
    overlap_right = min(right1, right2)
    overlap_top = min(top1, top2)

    overlap_height = max(0, (overlap_top - overlap_bottom))
    overlap_width = max(0, (overlap_right - overlap_left))

    return overlap_height * overlap_width

assert overlap((1, 1, 4, 4), (2, 2, 3, 3)) == 1.0
assert overlap((1, 1, 4, 4), (2, 2, 3, 4.5)) == 2.0
assert overlap((1, 1, 4, 4), (2, 2, 4.5, 4.5)) == 4.0
assert overlap((1, 1, 4, 4), (4.5, 4.5, 5, 5)) == 0.0
assert overlap((1, 1, 4, 4), (2.5, 4, 3.5, 4.5)) == 0.0
assert overlap((1, 1, 4, 4), (4, 4, 4.5, 4.5)) == 0.0

Note, we reran our other tests, to check our fix didn’t break something else. (We call that “fallout”)

Boundary cases#

“Boundary cases” are an important area to test:

  • Limit between two equivalence classes: edge and corner sharing fields

  • Wherever indices appear, check values at 0, N, N+1

  • Empty arrays:

    atoms = [read_input_atom(input_atom) for input_atom in input_file]
    energy = force_field(atoms)

  • What happens if atoms is an empty list?

  • What happens when a matrix/data-frame reaches one row, or one column?

Positive and negative tests#

  • Positive tests: code should give correct answer with various inputs

  • Negative tests: code should behave appropriately* given invalid inputs, rather than lying

*(It is up to you to decide what is “appropriate” behaviour in your context.)

Bad input should be expected and should fail early and explicitly.
Testing should ensure that explicit failures do indeed happen.

Raising exceptions#

In Python, we can signal an error state by raising an error:

def I_only_accept_positive_numbers(number):
    # Check input
    if number < 0:
        raise ValueError("Input " + str(number) + " is negative")

    # Do something

I_only_accept_positive_numbers(5)

I_only_accept_positive_numbers(-5)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[24], line 1
----> 1 I_only_accept_positive_numbers(-5)

Cell In[22], line 4, in I_only_accept_positive_numbers(number)
      1 def I_only_accept_positive_numbers(number):
      2     # Check input
      3     if number < 0:
----> 4         raise ValueError("Input " + str(number) + " is negative")

ValueError: Input -5 is negative

There are standard “Exception” types, like ValueError we can raise (more on this in Module 08.03)

We would like to be able to write tests like this:

assert I_only_accept_positive_numbers(-5) == # Gives a value error

But to do that, we need to learn about more sophisticated testing tools, called “test frameworks”.

A note on Test-Driven Development (TDD)#

In the overlapping fields example above we planned some of our test scenarios before writing the overlap function. This is an example of “Test-Driven Development (TDD)”. This was a particularly fashionable approach to development a few years ago. Some TDD advocates have taken an uncompromising approach which has led to it slightly falling out of favour more recently. However, it is worth retaining the benefits that caused its initial popularity.

In its “purest”/uncompromising form:

  • Always write and commit your tests before the related production code.

  • Always write tests to cover every line of your production code (we’ll cover how to measure this in the next module).

A more pragmatic interpretation might be:

  • Write your tests simultaneously with your production code.

  • Allow your tests to affect the design of your production code - i.e. ensure that your production code is testable.

  • When you are stuck, break down the problem into smaller, testable stages.

  • Ensure that your tests cover (i) the core function of the software and (ii) any input sanity checking.