9.2 Optimising with NumPy
Contents
9.2 Optimising with NumPy#
Estimated time for this notebook: 30 minutes
If we have our values in a numpy ndarray, we apply operations to each element in the array in one go, without having to loop over it.
9.2.1 Operations on arrays#
First, we want a ndarray containing the complex values that we previously used as input to our function.
xmin = -1.5
ymin = -1.0
xmax = 0.5
ymax = 1.0
resolution = 300
xstep = (xmax - xmin) / resolution
ystep = (ymax - ymin) / resolution
xs = [(xmin + xstep * i) for i in range(resolution)]
ys = [(ymin + ystep * i) for i in range(resolution)]
# list with complex values
cs_listcomp = [[(x + y * 1j) for x in xs] for y in ys]
import numpy as np
cs = np.asarray(cs_listcomp)
cs.shape
(300, 300)
We now want to compare adding a constant to every element of the array by
using a for loop
using numpy operators.
# we need to make copies of array to avoid overwriting it
cs_loop = cs.copy()
cs_numpy = cs.copy()
%%timeit
for i in range(cs_loop.shape[0]):
for j in range(cs_loop.shape[1]):
cs_loop[i][j] = cs_loop[i][j] + 10
34.3 ms ± 424 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Sometimes, you can use operators such as + as if we were dealing with single values. This is because the Numpy ndarrays have overridden the __add__ operation.
%%timeit
cs_numpy + 10
46.2 µs ± 96 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
But most Python functions do not know how to handle multi-dimensional arrays so we’ll use Numpy implementations where they exist.
import math
math.sqrt(cs)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[8], line 3
1 import math
----> 3 math.sqrt(cs)
TypeError: only size-1 arrays can be converted to Python scalars
np.sqrt(cs)
array([[0.38908588-1.28506335j, 0.38980707-1.28268581j,
0.39053184-1.28030535j, ..., 0.89141291-0.56090729j,
0.89409221-0.55922644j, 0.8967725 -0.55755501j],
[0.38670802-1.2843454j , 0.38742629-1.2819643j ,
0.38814812-1.27958025j, ..., 0.88972681-0.55822378j,
0.89241558-0.55654191j, 0.89510532-0.55486953j],
[0.38432663-1.28363038j, 0.38504193-1.28124573j,
0.3857608 -1.27885811j, ..., 0.88803965-0.55553075j,
0.89073797-0.55384788j, 0.89343724-0.55217458j],
...,
[0.38194169+1.28291834j, 0.38265402+1.28053014j,
0.3833699 +1.27813894j, ..., 0.88635146+0.55282811j,
0.88905943+0.55114426j, 0.8917683 +0.54947008j],
[0.38432663+1.28363038j, 0.38504193+1.28124573j,
0.3857608 +1.27885811j, ..., 0.88803965+0.55553075j,
0.89073797+0.55384788j, 0.89343724+0.55217458j],
[0.38670802+1.2843454j , 0.38742629+1.2819643j ,
0.38814812+1.27958025j, ..., 0.88972681+0.55822378j,
0.89241558+0.55654191j, 0.89510532+0.55486953j]])
9.2.2 Attempt 1: Binary Mandelbrot#
Numpy allows us to perform an iteration for our series on all complex values we’re interested in in a single line.
z0 = cs
z1 = z0 * z0 + cs
z2 = z1 * z1 + cs
z3 = z2 * z2 + cs
So can we just apply our mandel function to the whole matrix?
def mandel(constant, max_iterations=50):
"""Computes the values of the series for up to a maximum number of iterations.
The function stops when the absolute value of the series surpasses 2 or when it reaches the maximum
number of iterations.
Returns the number of iterations.
"""
value = 0
counter = 0
while counter < max_iterations:
if abs(value) > 2:
break
value = (value * value) + constant
counter = counter + 1
return counter
assert mandel(0) == 50
assert mandel(3) == 1
assert mandel(0.5) == 5
mandel(cs)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[12], line 1
----> 1 mandel(cs)
Cell In[11], line 14, in mandel(constant, max_iterations)
12 counter = 0
13 while counter < max_iterations:
---> 14 if abs(value) > 2:
15 break
17 value = (value * value) + constant
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
Looking at the error message, we learn a few things:
There’s a problem with line 14, where we check if the value of the series has divereged.
There’s some confusion about the truth value of our array. Our array has more than one element (300 x 300 elements to be precise), and the
ifcondition on line 14 returnsTruefor some elements andFalsefor others. But what doesTruemean for the entire array: Does every element have to beTrueor is it enough if any element isTrue? Since there’s no good answer to this, an error is raised.
What if we just apply the Mandelbrot algorithm without checking for divergence until the end:
def mandel_numpy_explode(constants, max_iterations=50):
"""Has the series diverged after all iterations?
Returns an array with True if the series doesn't explode and False otherwise.
"""
value = np.zeros(constants.shape)
counter = 0
while counter < max_iterations:
value = (value * value) + constants
counter = counter + 1
return abs(value) < 2
result_numpy_explode = mandel_numpy_explode(cs)
/tmp/ipykernel_16616/3334138926.py:11: RuntimeWarning: overflow encountered in multiply
value = (value * value) + constants
/tmp/ipykernel_16616/3334138926.py:11: RuntimeWarning: invalid value encountered in multiply
value = (value * value) + constants
We get an Overflow warning that we shouldn’t ignore. The overflow is caused by some values in the series exploding and running off to \(\infty\).
Go to notebook 9.6 Classroom Exercises and do Exercise 9c to fix the overflow issue.
9.2.3 Attempt 2: Return iterations#
The function mandel_binary (see Exercise 9c) runs on an array and is faster than our previous implementations. At the moment, it returns a boolean value for each element of the input: True if the element is in the Mandelbrot set, False otherwise.
It would be nice if the function returned, as before, the number of iterations that were performed. Let’s modify the function to do exactly that:
def mandel_numpy(constants, max_iterations=50):
"""Computes the values of the series for up to a maximum number of iterations.
The function stops values from exploding once diverged.
Returns the number of iterations.
"""
value = np.zeros(constants.shape)
# An array which keeps track of the first step at which each position diverged
diverged_at_count = np.ones(constants.shape) * max_iterations
counter = 0
while counter < max_iterations:
value = value * value + constants
diverging = abs(value) > 2
# Any positions which are:
# - diverging
# - haven't diverged before
# are diverging for the first time
first_diverged_this_time = np.logical_and(
diverging, diverged_at_count == max_iterations
)
# Update diverged_at_count for all positions which first diverged at this step
diverged_at_count[first_diverged_this_time] = counter
# Reset any divergent values to exactly 2
value[diverging] = 2
counter = counter + 1
return diverged_at_count
assert mandel_numpy(np.asarray([0])) == np.asarray([50])
assert mandel_numpy(np.asarray([4])) == np.asarray([0])
%%timeit
mandel_numpy(cs)
53.2 ms ± 82.2 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
result_numpy = mandel_numpy(cs)
import matplotlib.pyplot as plt
plt.set_cmap("cividis")
plt.xlabel("Real")
plt.ylabel("Imaginary")
plt.imshow(
result_numpy, interpolation="none", extent=[xmin, xmax, ymin, ymax], origin="lower"
)
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x7f844267c3a0>
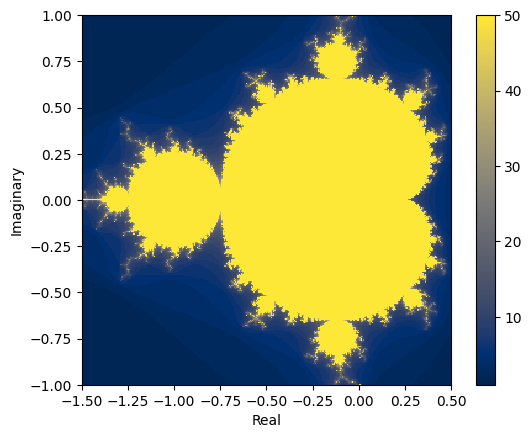
Even though we’re doing unnecessary calculations (compared to our pure Python implementation), we are much faster.

