9.5 Performance Scaling for Containers and Algorithms

Estimated time for this notebook: 15 minutes

9.5.0 Python Lists vs NumPy Arrays

We’ve seen that NumPy arrays are really useful. Why wouldn’t we always want to use them for data which is all the same type?

from timeit import repeat

import numpy as np
from matplotlib import pyplot as plt

Let’s look at appending data to a NumPy array, compared to a plain Python list:

def time_append_to_ndarray(count):
    # the function repeat does the same that the `%timeit` magic
    # but as a function; so we can plot it.
    return repeat(
        "np.append(before, [0])",
        f"import numpy as np; before=np.ndarray({count})",
        number=10000,
    )

help(repeat)

Help on function repeat in module timeit:

repeat(stmt='pass', setup='pass', timer=<built-in function perf_counter>, repeat=5, number=1000000, globals=None)
    Convenience function to create Timer object and call repeat method.

def time_append_to_list(count):
    return repeat("before.append(0)", f"before = [0] * {count}", number=10000)

counts = np.arange(1, 100000, 10000)


def plot_time(function, counts, title=None, top=None):
    plt.plot(counts, list(map(function, counts)))
    plt.ylim(bottom=0, top=top)
    plt.ylabel("seconds")
    plt.xlabel("array size")
    plt.title(title or function.__name__)

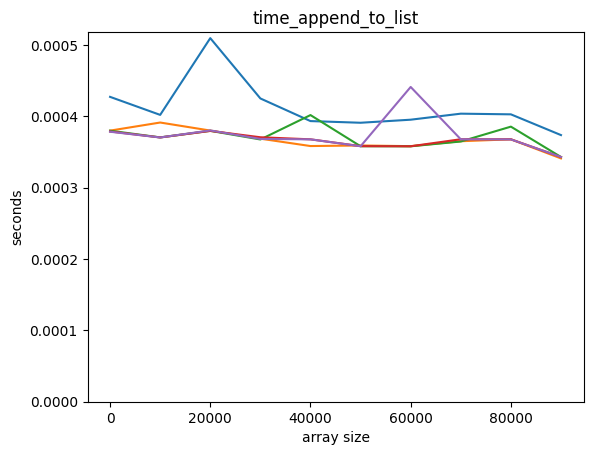
plot_time(time_append_to_list, counts)

plot_time(time_append_to_ndarray, counts)

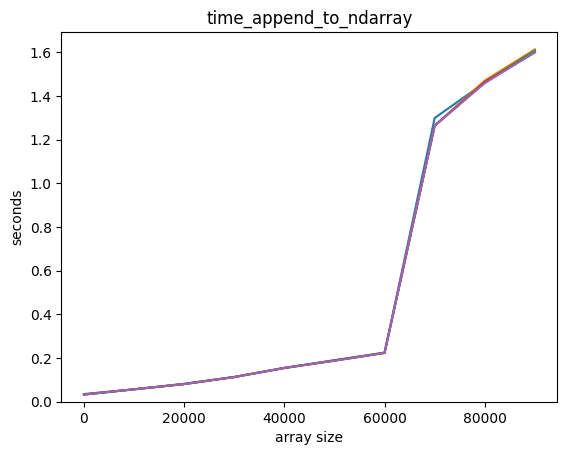
Adding an element to a Python list is way faster! Also, it seems that adding an element to a Python list is independent of the length of the list, but it’s not so for a NumPy array.

We would say that adding an element to a Python list is “constant time”. This is often written \(O(1)\)

We would say that adding an element to a Numpy array is “linear time”. This is written \(O(n)\).

If something is \(O(n + 1)\) then we shorten that to \(O(n)\) because the \(1\) becomes negligible as \(n\) grows very large.

\(O()\) or “big oh” notation is also used to describe the amount of memory required to perform some operation such as sorting.

Go to notebook 9.6 Classroom Exercises and do Exercise 9e.

More on optimising with numba in notebook: 9.8 Self study.