Recap example: Monte-Carlo#

Problem: Implement and test a simple Monte-Carlo algorithm#

Given an input function (energy) and starting point (density) and a temperature \(T\):

Compute energy at current density.
Move randomly chosen agent randomly left or right.
Compute second energy.
Compare the two energies:
If second energy is lower, accept move.
\(\beta\) is a parameter which determines how likely the simulation is to move from a ‘less favourable’ situation to a ‘more favourable’ one.
Compute \(P_0=e^{-\beta (E_1 - E_0)}\) and \(P_1\) a random number between 0 and 1,
If \(P_0 > P_1\), do the move anyway.
Repeat.

the algorithm should work for (m)any energy function(s).
there should be separate tests for separate steps! What constitutes a step?
tests for the Monte-Carlo should not depend on other parts of code.
Use matplotlib to plot density at each iteration, and make an animation

NB. If you are using the Windows command prompt, you will have to replace all %%bash directives in this notebook with %%cmd

Exercise - Partial Solution#

We have given you a partial solution below. In the solution we have broken the problem down into pieces:

A function to generate a random change: random_agent(), random_direction()
A function to compute the energy before the change and after it: energy()
A function to determine the probability of a change given the energy difference (1 if decreases, otherwise based on exponential): change_density()
A function to determine whether to execute a change or not by drawing a random numberaccept_change()
A method to iterate the above procedure: step()

Exercise: Fill in the gaps for testing

Input insanity: We have provided some unittests can provide a range of possible valid and invalid inputs. Add the production code necessary to handle these senarios elegantly.
We have provide the production code for change_density() and accept_change(). Add tests to ensure these functions work as expected. Consider these senarios:

change_density(): density is change by a particle hopping left or right? Do all positions have an equal chance of moving?
accept_change() will move be accepted when second energy is lower?

%%bash
rm -rf DiffusionExercise
mkdir DiffusionExercise

Windows: You will need to run the following instead

%%cmd
rmdir /s DiffusionExercise
mkdir DiffusionExercise

%%writefile DiffusionExercise/MonteCarlo.py
import matplotlib.pyplot as plt
from numpy import sum, array
from numpy.random import randint, choice


class MonteCarlo:
    """A simple Monte Carlo implementation"""

    def __init__(self, energy, density, temperature=1, itermax=1000):
        from numpy import any, array

        # ADD CODE HERE
        # Sanitise your inputs
        
        density = array(density)
        self.itermax = itermax

        self.current_energy = energy(density)
        self.temperature = temperature
        self.density = density

    def random_direction(self):
        return choice([-1, 1])

    def random_agent(self, density):
        # Particle index
        particle = randint(sum(density))
        current = 0
        for location, n in enumerate(density):
            current += n
            if current > particle:
                break
        return location

    def change_density(self, density):
        """Move one particle left or right."""

        location = self.random_agent(density)

        # Move direction
        if density[location] - 1 < 0:
            return array(density)
        if location == 0:
            direction = 1
        elif location == len(density) - 1:
            direction = -1
        else:
            direction = self.random_direction()

        # Now make change
        result = array(density)
        result[location] -= 1
        result[location + direction] += 1
        return result

    def accept_change(self, prior, successor):
        """Returns true if should accept change."""
        from numpy import exp
        from numpy.random import uniform

        if successor <= prior:
            return True
        else:
            return exp(-(successor - prior) / self.temperature) > uniform()

    def step(self):
        iteration = 0
        while iteration < self.itermax:
            new_density = self.change_density(self.density)
            new_energy = energy(new_density)

            accept = self.accept_change(self.current_energy, new_energy)
            if accept:
                self.density, self.current_energy = new_density, new_energy
            iteration += 1

        return self.current_energy, self.density


def energy(density, coefficient=1):
    """Energy associated with the diffusion model
    :Parameters:
    density: array of positive integers
    Number of particles at each position i in the array/geometry
    """
    from numpy import array, any, sum

    # Make sure input is an array
    density = array(density)

    # of the right kind (integer). Unless it is zero length, in which case type does not matter.
    if density.dtype.kind != "i" and len(density) > 0:
        raise TypeError("Density should be an array of *integers*.")
    # and the right values (positive or null)
    if any(density < 0):
        raise ValueError("Density should be an array" + "of *positive* integers.")
    if density.ndim != 1:
        raise ValueError(
            "Density should be an a *1-dimensional*" + "array of positive integers."
        )

    return coefficient * 0.5 * sum(density * (density - 1))

Writing DiffusionExercise/MonteCarlo.py

import sys

sys.path.append("DiffusionExercise")
import numpy as np
from IPython.display import HTML
from matplotlib import animation
from matplotlib import pyplot as plt
from MonteCarlo import MonteCarlo, energy

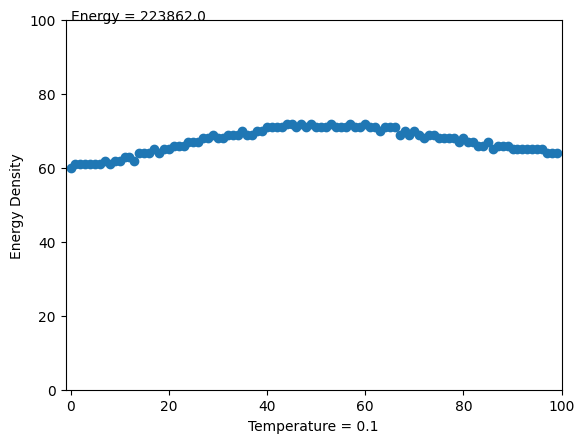
Temperature = 0.1

density = [np.sin(i) for i in np.linspace(0.1, 3, 100)]
density = np.array(density) * 100
density = density.astype(int)

fig = plt.figure()
ax = plt.axes(xlim=(-1, len(density)), ylim=(0, np.max(density) + 1))
image = ax.scatter(range(len(density)), density)
txt_energy = plt.text(0, 100, "Energy = 0")
plt.xlabel("Temperature = 0.1")
plt.ylabel("Energy Density")


mc = MonteCarlo(energy, density, temperature=Temperature)


def simulate(step):
    energy, density = mc.step()
    image.set_offsets(np.vstack((range(len(density)), density)).T)
    txt_energy.set_text(f"Energy = {energy}")


anim = animation.FuncAnimation(fig, simulate, frames=200, interval=50)
HTML(anim.to_jshtml())

../_images/05_07_diffusion_example_12_1.png

%%writefile DiffusionExercise/test_model.py
from MonteCarlo import MonteCarlo
from unittest.mock import MagicMock
from pytest import raises, approx


def test_input_sanity():
    """Check incorrect input do fail"""
    energy = MagicMock()

    # What happens if the tempurture is Absolute Zero? Can any thing meaningful be calculated here?
    with raises(NotImplementedError) as exception:
        MonteCarlo(sum, [1, 1, 1], 0e0)
        
    # Tempurture cannot be negitive
    with raises(ValueError) as exception:
        MonteCarlo(energy, [1, 1, 1], temperature=-1e0)

    # What happens if we attempt to use a decimal density value?
    with raises(TypeError) as exception:
        MonteCarlo(energy, [1.0, 2, 3])
        
    # What happens if we attempt to use a negitive density value?
    with raises(ValueError) as exception:
        MonteCarlo(energy, [-1, 2, 3])

    # What happens if we attempt to use a 2D density array?
    with raises(ValueError) as exception:
        MonteCarlo(energy, [[1, 2, 3], [3, 4, 5]])

    # What happens if our density array is too short?
    with raises(ValueError) as exception:
        MonteCarlo(energy, [3])
        
    # What happens if our density array doesn't contain positive integers?   
    with raises(ValueError) as exception:
        MonteCarlo(energy, [0, 0])


def test_move_particle_one_over():
    """Check density is change by a particle hopping left or right."""
    from numpy import nonzero, multiply
    from numpy.random import randint

    energy = MagicMock()

    # ADD CODE HERE
    # Test mc.change_density() here
    assert False
    

def test_equal_probability():
    """Check particles have equal probability of movement."""
    from numpy import array, sqrt, count_nonzero

    energy = MagicMock()

    # ADD CODE HERE
    # Test mc.change_density() here
    assert False


def test_accept_change():
    """Check that move is accepted if second energy is lower"""
    from numpy import sqrt, count_nonzero, exp

    # Clue
    energy = MagicMock()
    mc = MonteCarlo(energy, [1, 1, 1], temperature=100.0)

    # ADD CODE HERE
    # Test mc.accept_change() here
    assert False
  

def test_main_algorithm():
    import numpy as np
    from numpy import testing
    from unittest.mock import Mock

    density = [1, 1, 1, 1, 1]
    energy = MagicMock()
    mc = MonteCarlo(energy, density, itermax=5)

    acceptance = [True, True, True, True, True]
    mc.accept_change = Mock(side_effect=acceptance)
    mc.random_agent = Mock(side_effect=[0, 1, 2, 3, 4])
    mc.random_direction = Mock(side_effect=[1, 1, 1, 1, -1])
    np.testing.assert_equal(mc.step()[1], [0, 1, 1, 2, 1])

Writing DiffusionExercise/test_model.py

%%bash
cd DiffusionExercise
pytest --cov || echo "test failed"

============================= test session starts ==============================

platform linux -- Python 3.8.18, pytest-7.4.4, pluggy-1.5.0

rootdir: /home/runner/work/rse-course/rse-course/module05_testing_your_code/DiffusionExercise

plugins: cov-4.1.0, anyio-4.4.0, pylama-8.4.1

collected 5 items

test_model.py FFFF.                                                      [100%]

=================================== FAILURES ===================================

______________________________ test_input_sanity _______________________________

    def test_input_sanity():

        """Check incorrect input do fail"""

        energy = MagicMock()

        # What happens if the tempurture is Absolute Zero? Can any thing meaningful be calculated here?

        with raises(NotImplementedError) as exception:

>           MonteCarlo(sum, [1, 1, 1], 0e0)

E           Failed: DID NOT RAISE <class 'NotImplementedError'>

test_model.py:12: Failed

_________________________ test_move_particle_one_over __________________________

    def test_move_particle_one_over():

        """Check density is change by a particle hopping left or right."""

        from numpy import nonzero, multiply

        from numpy.random import randint

        energy = MagicMock()

        # ADD CODE HERE

        # Test mc.change_density() here

>       assert False

E       assert False

test_model.py:48: AssertionError

____________________________ test_equal_probability ____________________________

    def test_equal_probability():

        """Check particles have equal probability of movement."""

        from numpy import array, sqrt, count_nonzero

        energy = MagicMock()

        # ADD CODE HERE

        # Test mc.change_density() here

>       assert False

E       assert False

test_model.py:59: AssertionError

______________________________ test_accept_change ______________________________

    def test_accept_change():

        """Check that move is accepted if second energy is lower"""

        from numpy import sqrt, count_nonzero, exp

        # Clue

        energy = MagicMock()

        mc = MonteCarlo(energy, [1, 1, 1], temperature=100.0)

        # ADD CODE HERE

        # Test mc.accept_change() here

>       assert False

E       assert False

test_model.py:72: AssertionError

---------- coverage: platform linux, python 3.8.18-final-0 -----------

Name            Stmts   Miss  Cover

-----------------------------------

MonteCarlo.py      60     17    72%

test_model.py      45     12    73%

-----------------------------------

TOTAL             105     29    72%

=========================== short test summary info ============================

FAILED test_model.py::test_input_sanity - Failed: DID NOT RAISE <class 'NotImplementedError'>

FAILED test_model.py::test_move_particle_one_over - assert False

FAILED test_model.py::test_equal_probability - assert False

FAILED test_model.py::test_accept_change - assert False

========================= 4 failed, 1 passed in 0.68s ==========================

test failed

Complete Solution#

When you’ve attempted the exercise, have a look at this completed example solution.

don't look yet

ready?

%%bash
rm -rf DiffusionSolution
mkdir DiffusionSolution

Windows: You will need to run the following instead

%%cmd
rmdir /s DiffusionSolution
mkdir DiffusionSolution

%%writefile DiffusionSolution/MonteCarlo.py
import matplotlib.pyplot as plt
from numpy import sum, array
from numpy.random import randint, choice


class MonteCarlo:
    """A simple Monte Carlo implementation"""

    def __init__(self, energy, density, temperature=1, itermax=1000):
        from numpy import any, array

        density = array(density)
        self.itermax = itermax

        if temperature == 0:
            raise NotImplementedError("Zero temperature not implemented")
        if temperature < 0e0:
            raise ValueError("Negative temperature makes no sense")

        if len(density) < 2:
            raise ValueError("Density is too short")
        # of the right kind (integer). Unless it is zero length,
        # in which case type does not matter.
        if density.dtype.kind != "i" and len(density) > 0:
            raise TypeError("Density should be an array of *integers*.")
        # and the right values (positive or null)
        if any(density < 0):
            raise ValueError("Density should be an array of" + "*positive* integers.")
        if density.ndim != 1:
            raise ValueError(
                "Density should be an a *1-dimensional*" + "array of positive integers."
            )
        if sum(density) == 0:
            raise ValueError("Density is empty.")

        self.current_energy = energy(density)
        self.temperature = temperature
        self.density = density

    def random_direction(self):
        return choice([-1, 1])

    def random_agent(self, density):
        # Particle index
        particle = randint(sum(density))
        current = 0
        for location, n in enumerate(density):
            current += n
            if current > particle:
                break
        return location

    def change_density(self, density):
        """Move one particle left or right."""

        location = self.random_agent(density)

        # Move direction
        if density[location] - 1 < 0:
            return array(density)
        if location == 0:
            direction = 1
        elif location == len(density) - 1:
            direction = -1
        else:
            direction = self.random_direction()

        # Now make change
        result = array(density)
        result[location] -= 1
        result[location + direction] += 1
        return result

    def accept_change(self, prior, successor):
        """Returns true if should accept change."""
        from numpy import exp
        from numpy.random import uniform

        if successor <= prior:
            return True
        else:
            return exp(-(successor - prior) / self.temperature) > uniform()

    def step(self):
        iteration = 0
        while iteration < self.itermax:
            new_density = self.change_density(self.density)
            new_energy = energy(new_density)

            accept = self.accept_change(self.current_energy, new_energy)
            if accept:
                self.density, self.current_energy = new_density, new_energy
            iteration += 1

        return self.current_energy, self.density


def energy(density, coefficient=1):
    """Energy associated with the diffusion model
    :Parameters:
    density: array of positive integers
    Number of particles at each position i in the array/geometry
    """
    from numpy import array, any, sum

    # Make sure input is an array
    density = array(density)

    # of the right kind (integer). Unless it is zero length, in which case type does not matter.
    if density.dtype.kind != "i" and len(density) > 0:
        raise TypeError("Density should be an array of *integers*.")
    # and the right values (positive or null)
    if any(density < 0):
        raise ValueError("Density should be an array" + "of *positive* integers.")
    if density.ndim != 1:
        raise ValueError(
            "Density should be an a *1-dimensional*" + "array of positive integers."
        )

    return coefficient * 0.5 * sum(density * (density - 1))

Writing DiffusionSolution/MonteCarlo.py

import sys

sys.path.append("DiffusionSolution")
import numpy as np
from IPython.display import HTML
from matplotlib import animation
from matplotlib import pyplot as plt
from MonteCarlo import MonteCarlo, energy

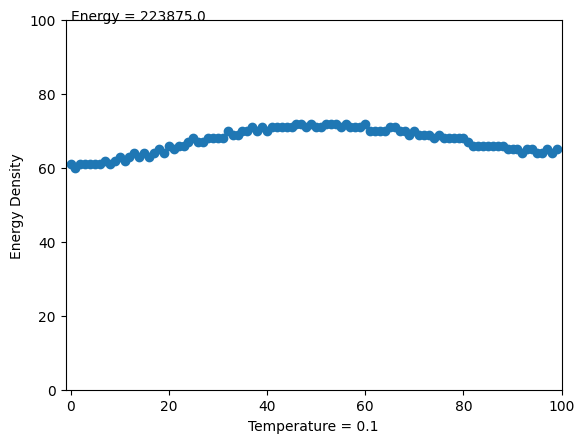
Temperature = 0.1

density = [np.sin(i) for i in np.linspace(0.1, 3, 100)]
density = np.array(density) * 100
density = density.astype(int)

fig = plt.figure()
ax = plt.axes(xlim=(-1, len(density)), ylim=(0, np.max(density) + 1))
image = ax.scatter(range(len(density)), density)
txt_energy = plt.text(0, 100, "Energy = 0")
plt.xlabel("Temperature = 0.1")
plt.ylabel("Energy Density")


mc = MonteCarlo(energy, density, temperature=Temperature)


def simulate(step):
    energy, density = mc.step()
    image.set_offsets(np.vstack((range(len(density)), density)).T)
    txt_energy.set_text(f"Energy = {energy}")


anim = animation.FuncAnimation(fig, simulate, frames=200, interval=50)
HTML(anim.to_jshtml())

../_images/05_07_diffusion_example_19_1.png

%%writefile DiffusionSolution/test_model.py
from MonteCarlo import MonteCarlo
from unittest.mock import MagicMock
from pytest import raises, approx


def test_input_sanity():
    """Check incorrect input do fail"""
    energy = MagicMock()

    with raises(NotImplementedError):
        MonteCarlo(sum, [1, 1, 1], 0e0)
    with raises(ValueError):
        MonteCarlo(energy, [1, 1, 1], temperature=-1e0)

    with raises(TypeError):
        MonteCarlo(energy, [1.0, 2, 3])
    with raises(ValueError):
        MonteCarlo(energy, [-1, 2, 3])
    with raises(ValueError):
        MonteCarlo(energy, [[1, 2, 3], [3, 4, 5]])
    with raises(ValueError):
        MonteCarlo(energy, [3])
    with raises(ValueError):
        MonteCarlo(energy, [0, 0])


def test_move_particle_one_over():
    """Check density is change by a particle hopping left or right."""
    from numpy import nonzero, multiply
    from numpy.random import randint

    energy = MagicMock()

    for i in range(100):
        # Do this n times, to avoid
        # issues with random numbers
        # Create density

        density = randint(50, size=randint(2, 6))
        mc = MonteCarlo(energy, density)
        # Change it
        new_density = mc.change_density(density)

        # Make sure any movement is by one
        indices = nonzero(density - new_density)[0]
        assert len(indices) == 2, "densities differ in two places"
        assert (
            multiply.reduce((density - new_density)[indices]) == -1
        ), "densities differ by + and - 1"


def test_equal_probability():
    """Check particles have equal probability of movement."""
    from numpy import array, sqrt, count_nonzero

    energy = MagicMock()

    density = array([1, 0, 99])
    mc = MonteCarlo(energy, density)
    changes_at_zero = [
        (density - mc.change_density(density))[0] != 0 for i in range(10000)
    ]
    assert count_nonzero(changes_at_zero) == approx(
        0.01 * len(changes_at_zero), 0.5 * sqrt(len(changes_at_zero))
    )


def test_accept_change():
    """Check that move is accepted if second energy is lower"""
    from numpy import sqrt, count_nonzero, exp

    energy = MagicMock()
    mc = MonteCarlo(energy, [1, 1, 1], temperature=100.0)
    # Should always be true.
    # But do more than one draw,
    # in case randomness incorrectly crept into
    # implementation
    for i in range(10):
        assert mc.accept_change(0.5, 0.4)
        assert mc.accept_change(0.5, 0.5)

    # This should be accepted only part of the time,
    # depending on exponential distribution
    prior, successor = 0.4, 0.5
    accepted = [mc.accept_change(prior, successor) for i in range(10000)]
    assert count_nonzero(accepted) / float(len(accepted)) == approx(
        exp(-(successor - prior) / mc.temperature), 3e0 / sqrt(len(accepted))
    )


def test_main_algorithm():
    import numpy as np
    from numpy import testing
    from unittest.mock import Mock

    density = [1, 1, 1, 1, 1]
    energy = MagicMock()
    mc = MonteCarlo(energy, density, itermax=5)

    acceptance = [True, True, True, True, True]
    mc.accept_change = Mock(side_effect=acceptance)
    mc.random_agent = Mock(side_effect=[0, 1, 2, 3, 4])
    mc.random_direction = Mock(side_effect=[1, 1, 1, 1, -1])
    np.testing.assert_equal(mc.step()[1], [0, 1, 1, 2, 1])

Writing DiffusionSolution/test_model.py

%%bash
cd DiffusionSolution
pytest

============================= test session starts ==============================

platform linux -- Python 3.8.18, pytest-7.4.4, pluggy-1.5.0

rootdir: /home/runner/work/rse-course/rse-course/module05_testing_your_code/DiffusionSolution

plugins: cov-4.1.0, anyio-4.4.0, pylama-8.4.1

collected 5 items

test_model.py .....                                                      [100%]

============================== 5 passed in 0.55s ===============================

Research Software Engineering with Python

Recap example: Monte-Carlo

Contents

Recap example: Monte-Carlo#

Problem: Implement and test a simple Monte-Carlo algorithm#

Exercise - Partial Solution#

Complete Solution#